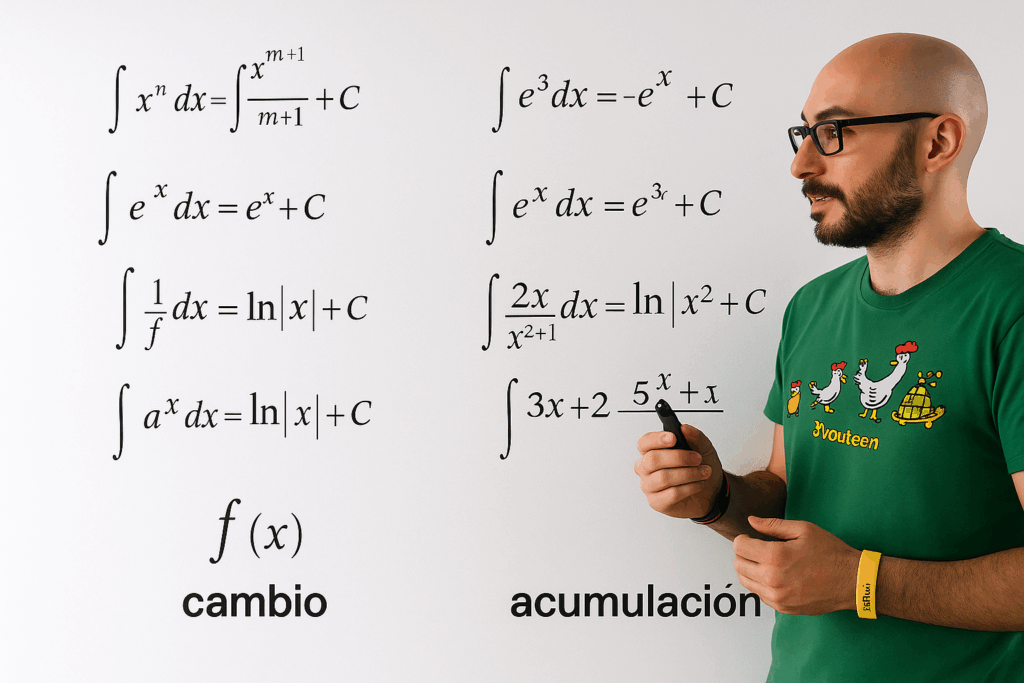¿Qué es una integral y por qué es importante?

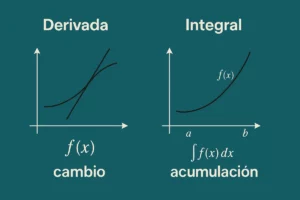
La integral es uno de los conceptos más relevantes en matemáticas, especialmente en cálculo. Así como la derivada mide el cambio, la integral mide la acumulación. En términos simples, mientras que la derivada responde a la pregunta “¿cuánto cambia algo?”, la integral responde “¿cuánto se ha acumulado hasta ahora?”.

Ejemplo práctico: Si tienes una función que representa la velocidad de un automóvil, su integral te dará la distancia recorrida. Esto demuestra cómo las integrales están directamente relacionadas con fenómenos cotidianos.

Si quieres profundizar en el concepto matemático, te recomiendo revisar la definicion formal de integral 

Tipos de integrales

Existen dos tipos principales de integrales que todo estudiante debe conocer:

1. Integrales indefinidas

Representan una familia de funciones. Por ejemplo:

∫ 2x dx = x² + C

Donde C es la constante de integración.

2. Integrales definidas

Calculan un valor numérico, normalmente el área bajo la curva entre dos puntos. Se escriben así:

∫[a,b] f(x) dx

Si quieres ver ejemplos gráficos, visita nuestro artículo sobre gráficas matemáticas.

Reglas básicas de integración

Las reglas de integración son, en cierto modo, el reverso de las reglas de derivación. Aquí tienes algunas esenciales:

• ∫ xⁿ dx = (xⁿ⁺¹)/(n+1) + C    (n ≠ -1)
• ∫ eˣ dx = eˣ + C
• ∫ 1/x dx = ln|x| + C
• ∫ cos x dx = sin x + C
• ∫ sin x dx = -cos x + C

Si quieres practicar estas fórmulas, puedes usar herramientas interactivas como Symbolab.

Métodos para resolver integrales paso a paso

No todas las integrales se pueden resolver aplicando directamente una fórmula. En esos casos existen técnicas muy útiles:

1. Sustitución

Se utiliza cuando una parte de la función parece ser la derivada de otra. Ejemplo:

∫ 2x cos(x²) dx

Si hacemos la sustitución u = x², entonces du = 2x dx. Así la integral se convierte en:

∫ cos(u) du = sin(u) + C

2. Integración por partes

Se aplica en productos de funciones, como x ln x. La fórmula general es:

∫ u dv = uv – ∫ v du

Si quieres ejemplos resueltos, revisa nuestra guía de integración por partes.

3. Fracciones parciales

Este método se usa con funciones racionales para descomponerlas en fracciones más simples y manejables.

4. Reconocimiento directo

A veces basta con identificar que la función ya contiene una “derivada escondida”. Este método requiere práctica y agudeza matemática.

Aplicaciones de las integrales en la vida real

Las integrales no son simples símbolos en un libro; tienen aplicaciones prácticas en distintas áreas:

• 📈 Economía: calcular ingresos y costos totales acumulados. Ver más en economía matemática.
• 🌊 Física: determinar desplazamientos, áreas, volúmenes y energía. Te recomiendo este artículo de apoyo: Uso de integrales en física.
• 💊 Biología: modelar crecimiento de poblaciones y dosis acumuladas de medicamentos.
• 💡 Ingeniería: medir presión, flujo, energía y transferencia de calor.

Cómo aprender integrales sin frustrarse

1. Empieza con lo visual: usa gráficas y diagramas para comprender la idea de acumulación.
2. Domina las reglas básicas: son pocas y se repiten constantemente.
3. Practica con ejemplos reales: aplica integrales a situaciones de tu vida o de tu carrera.
4. Busca apoyo: un profesor, mentor o curso online puede acelerar tu aprendizaje.

Si quieres aprender de forma estructurada, te recomiendo visitar nuestra sección de curso de cálculo.

Conclusión

Las integrales son mucho más que un tema de matemáticas: son la clave para comprender fenómenos de cambio y acumulación en la vida real. Con práctica constante, ejemplos visuales y un enfoque claro, dominar el cálculo integral es totalmente posible.

Recuerda: no se trata de complicarte, sino de aprender paso a paso hasta que las integrales se conviertan en una herramienta poderosa a tu favor.