Números fraccionarios: claves para comprender las fracciones desde la infancia

Uno de los temas de matemáticas que mayor dificultad genera en los niños durante los primeros años de colegio es el primer acercamiento a los números racionales. Un número racional se define como aquel que puede representarse como la división de dos números enteros. Al mencionar esta definición, muchos recuerdan inmediatamente sus primeros encuentros con las fracciones en la primaria.

En efecto, cuando hablamos de números racionales en el contexto escolar, nos referimos principalmente a los números fraccionarios, un contenido fundamental que sienta las bases para aprendizajes matemáticos más complejos.

Te puede interesar: Cómo aprender matemáticas.

¿Qué son los números fraccionarios o fracciones?

Los números fraccionarios son una forma de representar una cantidad dividida en partes iguales, sin necesidad de efectuar la división. Una fracción está compuesta por dos elementos:

• Numerador: se ubica en la parte superior y representa la cantidad que se toma.

• Denominador: se ubica en la parte inferior y representa en cuántas partes iguales se divide la unidad.

Ambos números están separados por una línea horizontal, conocida como barra de fracción.

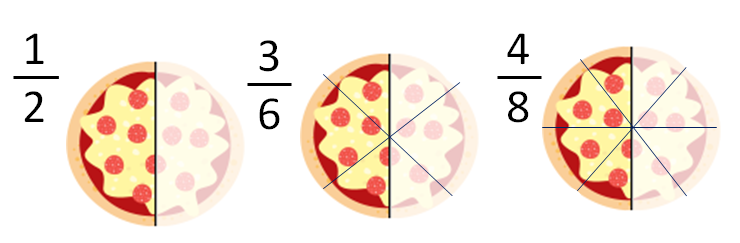
Por ejemplo, la fracción 2/5 (se lee dos quintos) representa una unidad dividida en cinco partes iguales, de las cuales se toman dos. Esta unidad puede ser un objeto, una cantidad o incluso una medida.

Las fracciones más allá de una división

Las fracciones no solo representan una división entre números enteros. También permiten expresar situaciones reales como:

• La cantidad de partes en que se divide un objeto.

• La proporción que se toma de un todo.

• La relación entre una parte y una unidad completa.

Gracias a esto, los números fraccionarios se convierten en una herramienta esencial para interpretar y resolver problemas cotidianos de manera precisa.

Te puede interesar: Cómo aprender matemáticas.

¿Dónde está la dificultad con los números fraccionarios?

Después de comprender el concepto básico, muchos estudiantes descubren que la verdadera dificultad no está en qué es una fracción, sino en realizar operaciones aritméticas con ellas, como:

• Suma de fracciones

• Resta de fracciones

• Multiplicación

• División

Estas operaciones suelen generar confusión, especialmente cuando se aplican a problemas asociados a situaciones de la vida diaria. Por ello, es fundamental reforzar la comprensión conceptual antes de avanzar a los procedimientos.

¿Por qué son tan importantes los números fraccionarios?

Los números fraccionarios están presentes constantemente en la vida cotidiana, incluso cuando no somos conscientes de ello. Algunas situaciones comunes donde se utilizan fracciones son:

• Repartir una pizza entre amigos.

• Comprar papel por cuartos, medios u octavos.

• Dividir una herencia entre varias personas.

• Comprar alimentos como queso o jamón por libras, medias libras o cuartos.

• Llenar un vehículo con gasolina por galones, medio galón o un cuarto.

Estos ejemplos muestran que comprender y usar adecuadamente las fracciones es una habilidad práctica y necesaria.

Fracciones y vida diaria

Sin los números fraccionarios, tareas como cocinar, repartir objetos, organizar eventos o realizar construcciones —desde las más simples hasta las más complejas— serían extremadamente difíciles. Las fracciones permiten medir, dividir, comparar y organizar cantidades de forma justa y precisa.

Por esta razón, una vida sin números fraccionarios sería muy distinta a la que conocemos hoy.

Conclusión

Los números fraccionarios son una pieza clave del aprendizaje matemático. Aunque pueden representar un reto inicial para los niños, una explicación clara, el uso de ejemplos cotidianos y la práctica constante permiten comprenderlos con mayor facilidad.

Fortalecer este conocimiento desde los primeros años escolares no solo mejora el desempeño académico, sino que también prepara a los estudiantes para resolver problemas reales de manera lógica y efectiva.